通过提高应力水平加速产品性能退化,获取产品在高应力水平下的性能退化数据,并利用这些数据来估计产品可靠性及预测产品在使用应力下的寿命时间的加速试验方法成为加速退化试验(ADT)。
加速退化试验可分为两种,分别为非破坏性加速退化试验和破坏性加速退化试验,本方法可用于破坏性加速退化试验评估。
产品性能指标值的退化速度随着温度的上升而按照指数函数规律增加;对于特征寿命来说,其值随着温度的上升而按照指数函数规律下降。可得线性化(对1/T)的Arrhenius模型:
幂律模型表明,产品性能指标值的反应速度或退化速度是应力的幂函数。线性化(对In S)的幂律模型:
就一般情况而言,如果引入性能指标值或退化量x的某个函数,则其与反应速度、退化速度的关系可以写为:
根据求得的样本均值、样本均方差或尺度参数、形状参数随时间变化的函数,根据实验所用应力种类,选择加速模型,利用最小二乘法求出参数曲线模型系数与应力水平的关系;
假定失效阈值为Df,利用上述得到的参数曲线方程系数与应力水平的关系,可以求出正常使用应力条件下,产品性能退化量的样本均值、样本均方差或尺度参数、形状参数随时间变化的函数关系;
基于退化量分布的加速退化数据可靠性评估方法的算法流程图如图1所示。
图1 基于退化量分布的加速退化数据可靠性评估方法的算法流程图
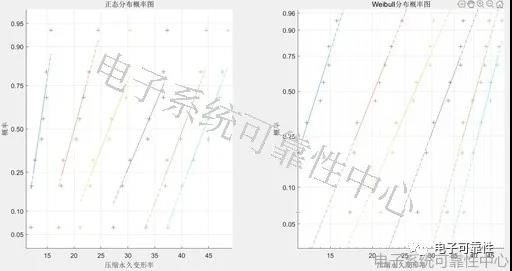
对于不同温度下,不同时刻性能退化数据进行分布假设检验,如图2所示,由图可以看出,不同时刻样本性能退化量基本服从正态分布,也符合服从Weibull分布,下面针对这两种分布对产品进行可靠性评估。
首先求出不同应力水平下、不同测量时刻产品的性能退化量的样本均值与样本均方差。一般时刻均值点估计采用极大似然估计(MLE),时刻均方差估计采用最小方差无偏估计(MVUE)。
可以利用MATLAB求出不同应力下性能退化量均值与样本均方差,画出产品退化量的样本均值与样本均方差随时间变化的曲线,如图3所示。
假设产品性能退化量均值与样本均方差方程系数与温度的关系满足Arrhenius加速模型。线性化Arrhenius模型为:
3.2假设不同时刻退化量服从Weibull分布时产品的可靠性评估
计算出不同应力水平下、不同测量时刻样本性能退化量的形状参数与尺度参数。以T=83℃、t=452时刻数据为例。
画出产品性能退化的尺度参数与形状参数随时间变化的曲线,如图4所示。
通过图4可以看出,该产品在不同应力下性能退化量的尺度参数为时间的线性函数,形状参数基本不变,因此可以利用最小二乘法求出它们在不同应力水平下随时间变化的函数如表4所示。
假设产品性能退化量的尺度参数方程系数及形状参数与温度的关系满足Arrhenius加速模型。
根据得到得可靠度函数,分别画出性能退化量服从正态分布与Weibull分布时得到的可靠的曲线如下:
对于不同温度下,不同时刻的压缩永久变形率进行分布假设检验,结果如图6所示。
4.2 假设不同时刻退化量服从Weibull分布时产品的可靠性评估
求出不同应力水平下,不同测量时间产品的性能退化量的尺度参数与形状参数,产品性能退化量的尺度参数与形状参数随时间变化的曲线如图8所示。
通过图8可以看出,该产品在不同应力下性能退化量的尺度参数为时间的线性函数,形状参数基本不变,因此可以利用最小二乘法求出它们在不同应力水平下随时间变化的函数如表6所示。
根据得到得可靠度函数,分别画出性能退化量服从正态分布与Weibull分布时得到的可靠的曲线如下: